第一章 绪论

以市场有效理论为基础的现代金融经济学引发了过去十年间从主动管理（试图战胜市场）向被动管理（试图复制市场）的大规模迁移。

1.1 主动管理和被动管理

主动投资和被动投资是投资管理中的两个重要概念，它们的主要区别在于投资组合的管理方式和投资目标。

主动投资是指投资者通过选择特定的资产和投资策略来试图跑赢市场，并获得超额收益。主动投资的管理方式通常是基于投资经理的研究和分析，以便在市场波动中寻找投资机会，并通过适当的风险管理策略来控制风险。主动投资的投资目标是打败市场基准，获得超过市场平均水平的回报。

被动投资是指投资者选择投资于跟踪特定市场指数或基准的投资工具，以便获得市场平均水平的回报。被动投资的管理方式通常是基于市场指数或基准的复制和调整，以便在投资组合中持有与市场指数或基准相同的资产。被动投资的投资目标是与市场基准相匹配，获得与市场基准相同的回报。

因此，主动投资和被动投资的主要区别在于投资组合的管理方式和投资目标。主动投资希望跑赢市场，获得超过市场平均水平的回报，需要投资经理进行主动的研究和分析；而被动投资则希望与市场基准相匹配，获得市场平均水平的回报，不需要投资经理进行主动的研究和分析，通常采用基于指数或基准的投资工具。

1.2 本书结构

在整部书中，我们将投资组合与收益率预测或资产特征关联起来。这个观点创新性地把完全不可比的几种资产特征转换到统一的维度（投资组合），并使用投资组合理论的工具来研究它们。

残差收益率（residual return）是资产收益率中与业绩基准收益率不相关的部分。信息率（information ratio，IR）是残差收益率的年化预期值与其年化波动率之比。

如何在不同的投资机会之间选择，取决于偏好（preference）。在主动管理中，更高的残差收益率、更低的残差风险是必然的偏好。我们采用均值/方差的方式来体现这一点，即用残差收益率减去一个残差风险的二次惩罚项（残差方差的线性惩罚项）。我们称之为“风险调整预期收益率”（risk-adjusted expected return）或“附加值”（value-added）。我们可以用无差异曲线来描述偏好。不同的均值/方差组合，只要它们的附加值相同，我们对它们的偏好就没有差异。每一条无差异曲线都包含一个具有零残差风险的特殊组合，其残差收益率被称为“确定性等价”残差收益率。

当我们同时考虑偏好（无差异曲线）与机会集时，就产生了投资选择。在主动管理中，可获得的最高附加值正比于信息率的平方。

信息率定义了主动投资经理可选的投资机会的集合。信息率越高，主动管理的空间越大。 在主动管理中，可获得的最高附加值正比于信息率的平方。

更高的信息率（IR）的来源：

• 更高的信息系数（IC）：预测每只股资产的残差收益率的能力
• 更大的广度（BR）：每年我们能够应用上述预测能力的次数

$IR = IC \cdot \sqrt{BR}$

主动管理即预测，预测是指将资产收益率的原始预测信号转化为精炼预测的过程。

阿尔法 = 波动率 · IC · 标准分值

那么，怎样的预期收益率模型在主动管理中被证实是有效的呢？一种方法是找出过去表现出色的资产的共同特征，进而找出那些将要表现出色的资产。另一种方法试图运用比较估值法来找出具有相同因子暴露但市场定价却不同的资产。一旦找到，意味着套利机会的出现。还有一种方法是去预测那些由市场定价的因子的收益率。

第二章 一致预期收益率：资本资产定价模型CAPM

2.1 导论

CAPM是预测预期收益的最好办法，还有一种办法是套利定价理论（APT），是一个主动投资经理的有效工具，但不能作为一致预期收益率的来源。

CAPM基于两个构想：第一个构想是市场组合M，第二个是将任何个股或组合与市场联系起来的贝塔系数的概念。

2.2 收益率分解

2.2.1 贝塔的定义

让我们考虑一个组合P，记组合P的超额收益率为$r_P$ ，市场M的超额收益率为$r_M$。超额收益是收益率减去同期无风险资产的收益率。我们定义组合P的贝塔系数为：

$\beta_P = \frac{Cov(r_P, r_M)}{Var(r_M)}$

即贝塔正比于组合收益率与市场收益率的协方差。协方差（Covariance）是描述两个随机变量之间关系的一种统计量，它度量的是它们的变化趋势是否一致。如果两个随机变量在一起变化的趋势是一致的，那么它们的协方差为正数；如果它们的趋势是相反的，那么协方差为负数；如果它们的趋势没有明显的一致性，那么协方差接近于0。

贝塔这个名字的来源是线性回归方程：组合P在时期t=1，2，3，……，T上的超额收益率$r_P(t)$ 对同期市场超额收益率$r_M(t)$ 回归，即

$r_P(t) = \alpha_P + \beta_P r_M(t) + \epsilon_P(t)$

我们把通过上述回归分析得到的对$\alpha_P$和$\beta_P$ 的估计值称为现实的/历史的阿尔法值和贝塔值，用于与他们的先验值进行区分。这个估计显示了组合P与市场组合在历史上的相互关系。历史贝塔值是对未来贝塔值的一个合理预测。

2.2.2 贝塔的意义

贝塔使我们能干将任意组合的超额收益率分解为两个不相关的部分，一个是市场部分，另一个是残差部分。

$r_P = \beta_P r_M + \theta_P$

此外，残差收益率$\theta_P$与市场收益率$r_M$ 是不相关的，所以组合P的方差亦可以分解为

$\sigma^2_P = \beta^2_P \sigma^2_M + \omega^2_P$

这里$\omega^2_P$ 是组合P的残差方差，即$\theta_P$ 的方差

2.3 CAPM

CAPM认为：任何股票或组合的预期残差收益率为零，即$E\{\theta_P\} = 0$。这意味着组合P的预期超额收益率（$E\{r_P\} = \mu_P$），完全由市场的预期超额收益率（$E\{e_M\} = \mu_M$）和贝塔的组合（$\beta_P$） 来决定， 他们之间的关系为：

$E\{r_P\} = \beta_P E\{r_M\} = \beta_P\mu_M$

CAPM背后的逻辑：

1. 投资者承担的必要风险会得到补偿，而承担的非必要风险则不会得到任何补偿。
2. 组合中的市场风险是必要的，市场风险无法避免，承担市场风险是组合收益的来源。
3. 残差风险是投资者自主承担的，是应该被规避的。

在CAPM下，持有异于市场组合的投资者在玩一个零和游戏，这类投资者承担了额外的风险却没有获得额外的预期收益，这个逻辑导致被动投资，即买入并持有市场组合。

有效市场理论

有效市场理论有三种强度：弱有效、半强有效和强有效

弱有效：只使用历史价格和成交量数据不能战胜市场； 半强有效：只使用公开信息不能战胜市场； 强有效：投资者无论如何都无法战胜市场，市场包含了一切相关信息

CAPM推论

根据CAPM，将收益率和风险分解为市场部分和残差部分的能力依赖于我们预测贝塔的能力。CAPM进一步确认任何股票（从而任何组合）的残预期残差收益率为0.

2.4 后验与先验

CAPM是关于预期的。如果对任给的一系列股票或组合，以其贝塔值为横坐标、CAPM预期年化收益率为纵坐标绘制在坐标系中，我们会发现它们都落在一条直线上：纵截距为无风险收益率$i_F$ ，斜率为市场的预期超额收益率$\mu_M$ 。这条直线被称为证券市场线 （security market line）（见图2-1）。

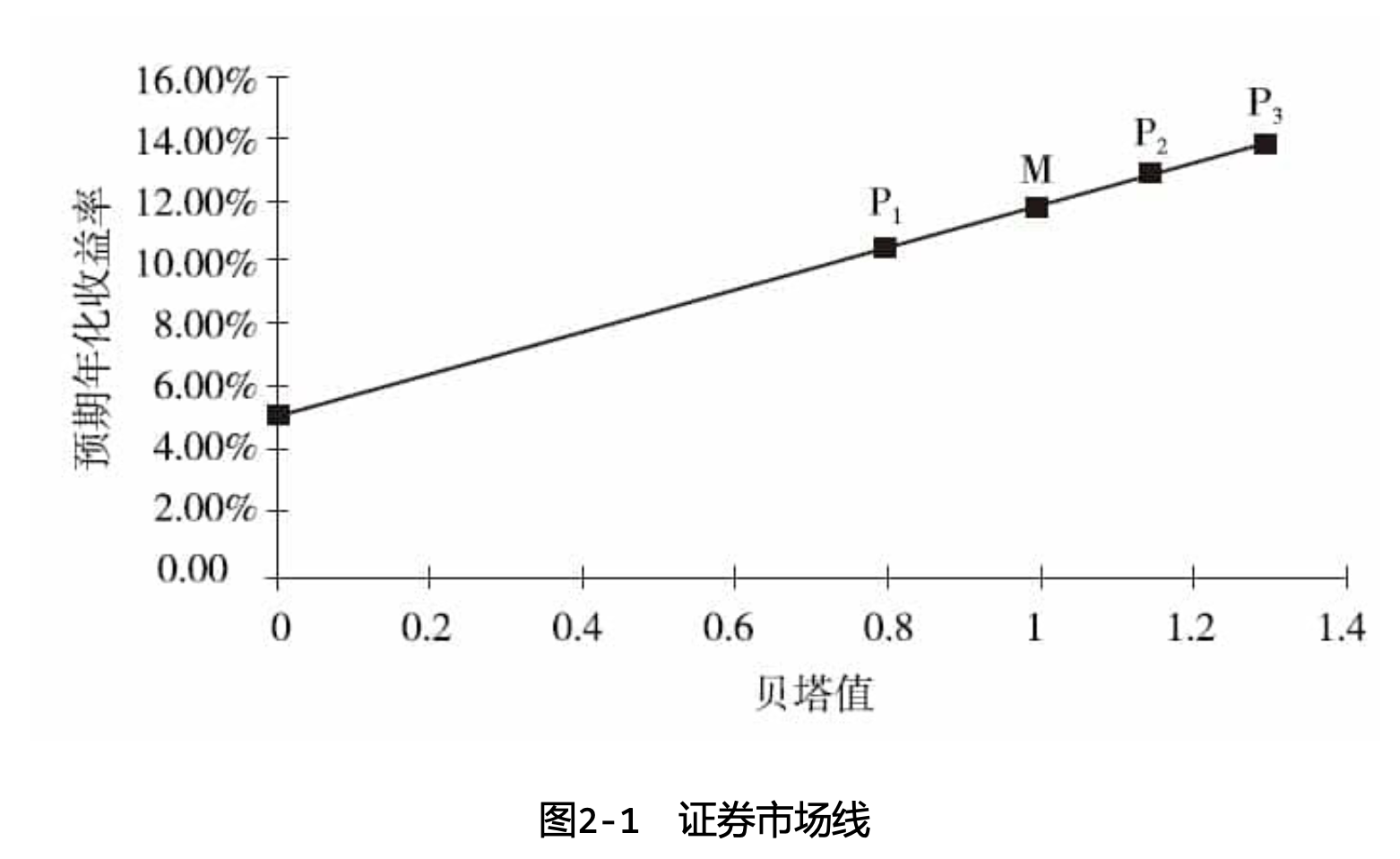
如果我们根据后验（ex post）或事后收益率（称为实现值）来重新绘制，我们将看到一张组合实际收益率对组合贝塔的散点图。图2-2展示了一张由三个样本组合、市场组合和无风险资产构成的散点图。我们总是可以用一条直线将无风险资产和市场组合（均由收益率和风险的实现值定位）连接起来。这条后验的“证券市场线”或可被称为“不稳定”（insecurity）市场线。这条后验直线给出了在假设我们知道市场组合收益率时，CAPM预测的那部分收益率。特别地，在市场收益率低于无风险收益率的时期上，这条直线将向右下方倾斜。

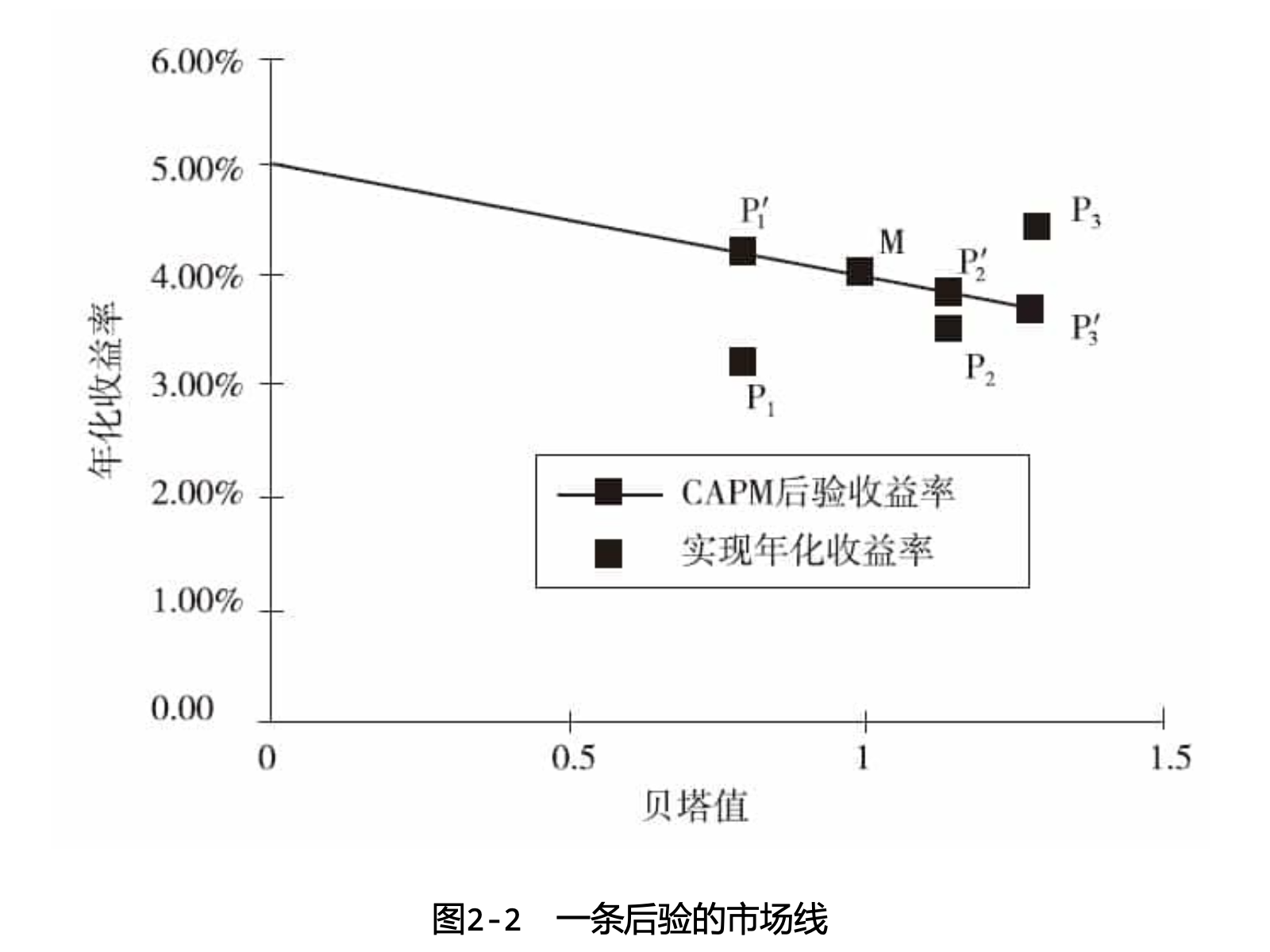
2.4 一个例子

作为CAPM分析的一个例子，让我们考虑主要市场指数（Major Market Index，MMI）的一只成分股美国邮政（American Express）在1988年1月~1992年12月（共60个月）相对于标普500指数的表现。图2-3是股票美国邮政月度超额收益率（y轴）对标普500指数月度超额收益率（x轴）的散点图。

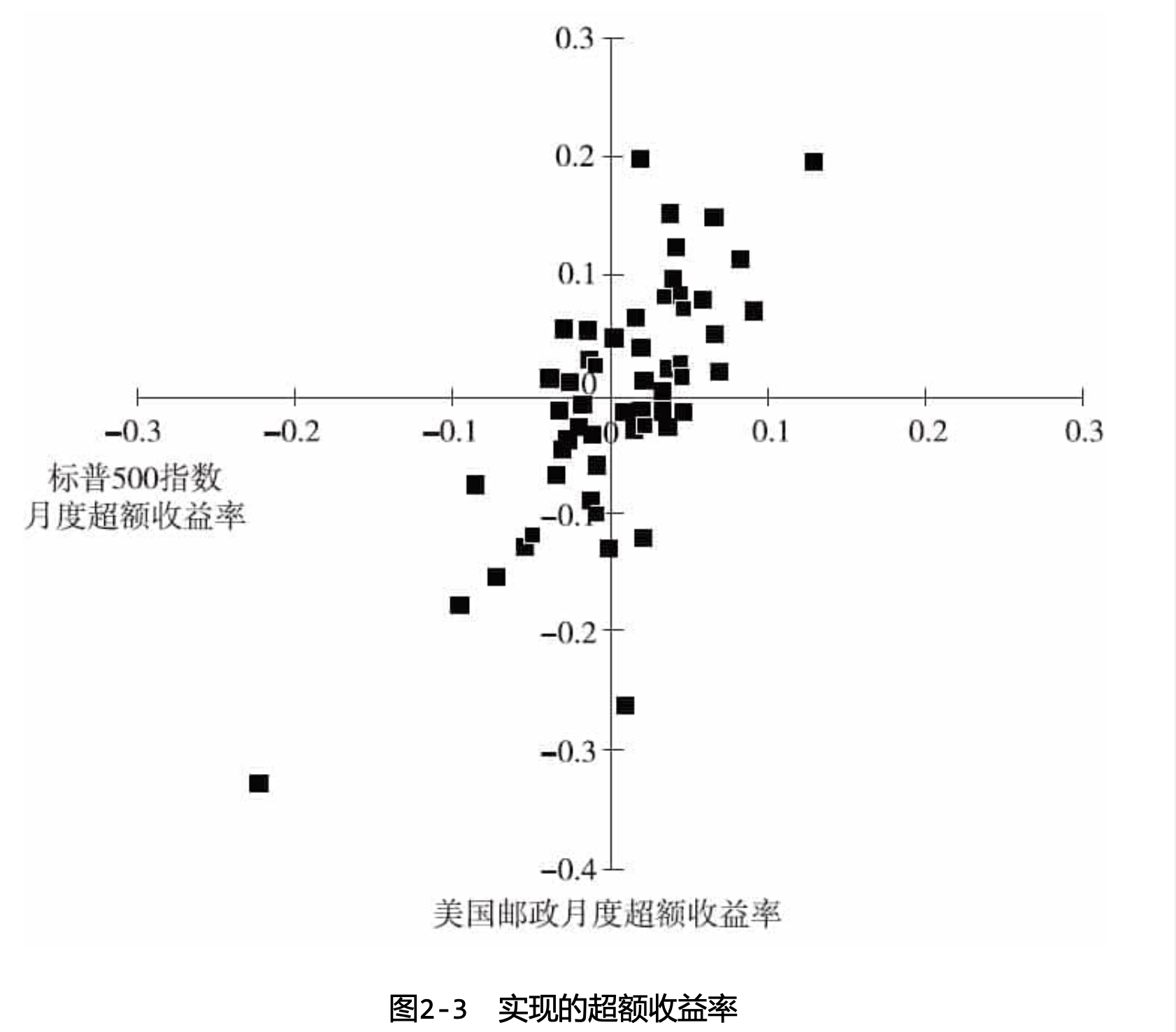
利用回归分析式（2-2），我们可以确定American Express的历史贝塔值为1.21，估计误差为0.24。我们知道，CAPM对残差收益率的先验预测值是零。而本例的后验结果是：在这段历史时期上，该股票的残差收益率的实现值为平均每月-78个基点（base point，万分之一），这个月均量的估计偏差是96个基点：在95%的置信水平下并不显著。月度残差收益率的标准差是7.05%。在此例中，回归的决定系数R 2 是0.31。

2.5 预测贝塔

CAPM对预期收益率的预测不会优于对贝塔的预测。 预测贝塔的方法有很多种。最简单的一种就是通过对历史收益率的分析得出历史贝塔。稍微复杂一些的方法是在历史贝塔上进行贝叶斯调整（Bayesian adjustment）。

第三章 风险

3.1 导论

预期收益率是主动管理中的积极因素，而风险是消极因素。

本章要点：

• 风险是收益率的标准差
• 风险不具备可加性
• 许多机构投资者关注主动风险和残差风险多于总风险
• 主动风险主要依赖于主动头寸的规模，而不是基准头寸的规模
• 风险造成的成本与方差成正比
• 风险模型识别重要的风险来源，并把风险分解为多个组成部分

3.2 风险定义——收益率的标准差

标准差衡量了收益率在均值附近分布范围的宽度。投资者通常称标准差为波动率（volatility）。方差是标准差的平方。

标准差是哈里·马科维茨（Harry Markowitz）对风险的定义，并且之后一直被机构投资界视为风险的标准定义。标准差的好处如下：

• 标准差有熟知的，清晰的统计属性，尤其适用于现有的投资组合构建工具。只需知道每只资产的标准差和资产之间的相关性，我们就能够计算出任何投资组合的标准差。
• 标准差随时间的变化相对稳定（尤其是和收益率均值以及收益率分布的其他矩相比），并且金融经济学家已经发展出精确预测标准差的有力工具。

半方差

对标准差的批评：标准差同时包含了收益率高于和低于均值的情形，而多数投资者认为较低的或者负的收益率才是风险（虽然卖空者持有相反的观点）。这就产生了一种新的风险定义：半方差 （semivariance）或下行风险 （downside risk）。

半方差的定义与方差类似，唯一区别在于半方差仅使用低于均值的收益率样本。如果收益率的分布是对称的，即收益率高于均值X%和低于均值X%的概率相等，那么半方差将恰等于方差的一半。

人们对下行风险的定义却不统一；一种类比标准差和方差之间关系的定义方式是：将下行风险定义为半方差的平方根。

目标半方差

半方差的一种变体是目标半方差 （target semivariance）。半方差关注低于均值的收益率样本，而目标半方差将关注低于某一目标收益率的样本。

下行风险本身也有一些问题。第一，它的定义不像标准差或方差那样明确，且其统计属性并不熟知。第二， 大规模投资组合的下行风险在计算上非常挑战，因为把下行风险从单只资产汇总到组合很难做好。第三，如果投资收益率的分布是对称的，下行风险的大多数定义仅仅是标准差或者方差的一个固定倍数，并不蕴含额外的信息。我们知道，主动收益率（相对于业绩基准）根据其定义应该是对称的。

另外，我们在估计下行风险时仅用到一半的样本，于是会损失统计精度。这个问题对目标半方差的影响更大，因为目标半方差通常更加关注于分布“尾部”的样本。

损失概率

损失概率 （shortfall probability）是另一种风险定义，它可能是最接近人们对风险的直观感受的定义。损失概率是收益率落在目标值以下的概率。损失概率具有接近风险直观感受的优点，然而，它面临着与下行风险一样的问题：定义模糊、不为人熟知的统计属性、难于预测以及依赖于投资者的个人偏好等。

在险价值

在险价值 （value at risk）是与损失概率类似的一种风险定义。损失概率先取定目标损失值，然后计算收益率低于该数值的概率；而在险价值先取定一个目标概率，例如1%或者5%，然后计算与该概率相应的收益率分位数。例如麦哲伦基金，其最差的1%的月度收益率的亏损超过了20.8%。也就是说，如果投资1000美元于麦哲伦基金，那么在险价值为208美元。

3.3 分散化来降低风险

整体风险小于部分风险之和——这是投资组合分散化的关键

如上所述，能够满足我们普适、对称、灵活和可精确预测要求的风险定义就是收益率的标准差。如果用$R_P$ 表示一个投资组合的总收益（例如总收益等于1.10意味着投资组合的收益率是10%），那么该组合收益率的标准差表示为$\sigma_P = Std\{R_P\}$。

一个投资组合的超额收益率$r_P$ 定义为其总收益$R_P$ 与无风险资产的总收益$R_F$ （例如若国库券收益率为4%，那么$R_F$ =1.04）之差。由于无风险资产的总收益$R_F$ 是在考察期期初就确定下来的，所以超额收益率的风险总是等于总收益的风险。若无特殊说明，我们讨论的风险总是指收益率的年化标准差（以百分之一为单位）。

标准差具有一些有趣的特点。特别地，它不具有组合属性，也即投资组合的标准差不等于组合中各资产标准差的加权平均值。

假设股票1和股票2的收益率的相关系数为$\rho_{12}$ ，来考察一个投资组合P，它由50%的股票1和50%的股票2构成，那么

$\sigma_P = \sqrt{(0.5\sigma_1)^2 + (0.5\sigma_2)^2 + 2(0.5\sigma_1)(0.5\sigma_2)\rho_{12}}$

并且

$\sigma_P \leq 0.5\sigma_1 + 0.5\sigma_2$

其中式（3-2）等号成立当且仅当这两只股票完全相关（即ρ 12 =1）。式（3-2）说明：整体风险小于部分风险之和——这是投资组合分散化的关键。

Ex-1

考虑一个由N只股票构成的等权重投资组合，每只股票的风险都是σ，并且股票之间互不相关。那么，该组合的风险是

$\sigma_P = \frac{\sigma}{\sqrt{N}}$

可以发现，本例中股票的平均风险是$\sigma$，但投资组合的风险为$\sigma/\sqrt{N}$

Ex-2

再来考虑一个更接近现实的分散化的例子。这次我们假设任意两只股票的收益率之间的相关系数都等于ρ；那么一个包含N只股票的等权重投资组合的风险是

$\sigma_P = \sigma\sqrt{\frac{1+\rho(N-1)}{N}}$

当组合中的股票数N很大时，上式变为

$\sigma_P \to \sigma\sqrt{\rho}$

3.4 风险年化

风险既不能沿横截面也不能沿时间相加。然而方差可以沿时间相加，如果任意不重叠的两段时期上的收益率是不相关的。事实上，对于大多数资产类型而言，其前后两段不重叠时期上的收益率之间的相关性，即自相关性（auto-correlation），都是接近于0的。这意味着方差随着预测期的长度增长，而风险随着预测期长度的平方根增长。

每次将风险“年化”（即将风险数值换算到年度区间上）时，我们都会使用上述关系。如果我们考察一只股票的月度收益率，并且观测到其月度收益率的标准差为σ 月度 ，那么我们将按下式把它换算为年化风险：

$\sigma_{年度} = \sqrt{12} \sigma_{月度}$

3.5 主动风险

如果将一位投资经理的业绩与一个业绩基准做比较，那么该经理的投资组合的超额收益率$r_P$ 与业绩基准的超额收益率$r_B$ 之间的差异将至关重要。我们称这个差异为主动收益率（active return），记为$r_{PA}$ 。相应地，我们定义主动风险$\psi_{P}$ 为主动收益率的标准差：

$\psi_P =Std\{r_{PA}\}=Std\{r_P -r_B \}$

我们有时也称主动风险为跟踪误差 （tracking error），因为它描述了组合对业绩基准的跟踪效果。

很多投资者认为：资产的主动风险与其市值成比例。因此，如果IBM的市值在业绩基准中所占权重是4%，他们就会对其头寸设置2%的下限和6%的上限，以对应于50%的超配和50%的低配。对另一只市值在业绩基准中所占权重仅有0.6%的股票，他们会为其头寸设置0.3%的下限和0.9%的上限。于是，他们将自己对IBM的主动暴露限制在±2%，而将自己对另一只股票的主动暴露限制在±0.3%。然而，主动风险取决于主动暴露和股票风险，并不依赖于该股票在业绩基准中的权重。也就是说，在大盘股上1%的主动暴露并不一定比在小盘股上1%的主动暴露风险更低。有时我们对大盘股的主动暴露设置更少的限制，是出于交易成本和流动性方面的考虑。

3.6 残差风险

残差风险是收益率中与系统性收益率正交的那部分的风险。组合P关于组合B的残差风险用$\omega_P$ 表示，定义为

$\omega_P = \sqrt{\sigma_P^2 - \beta_P^2\sigma_B^2}$

其中

$\beta_P = \frac{Cov\{r_P, r_B\}}{Var\{r_B\}}$

贝塔的中位数不必等于1，只有贝塔的市值加权平均值等于1。

方差是标准差的平方。本书中我们将统一使用方差来衡量风险的成本。风险成本将风险换算为等价的预期收益率折损。在主动管理的讨论中，风险成本通常与主动风险或残差风险相关联。图3-4展示了主动风险厌恶系数取0.1时，主动风险产生的成本与主动风险的关系。在这样的主动风险厌恶水平下，4%的主动风险将换算为0.1×4 2 =1.6%（我们约定风险厌恶系数乘在百分数上）的预期收益率折损。

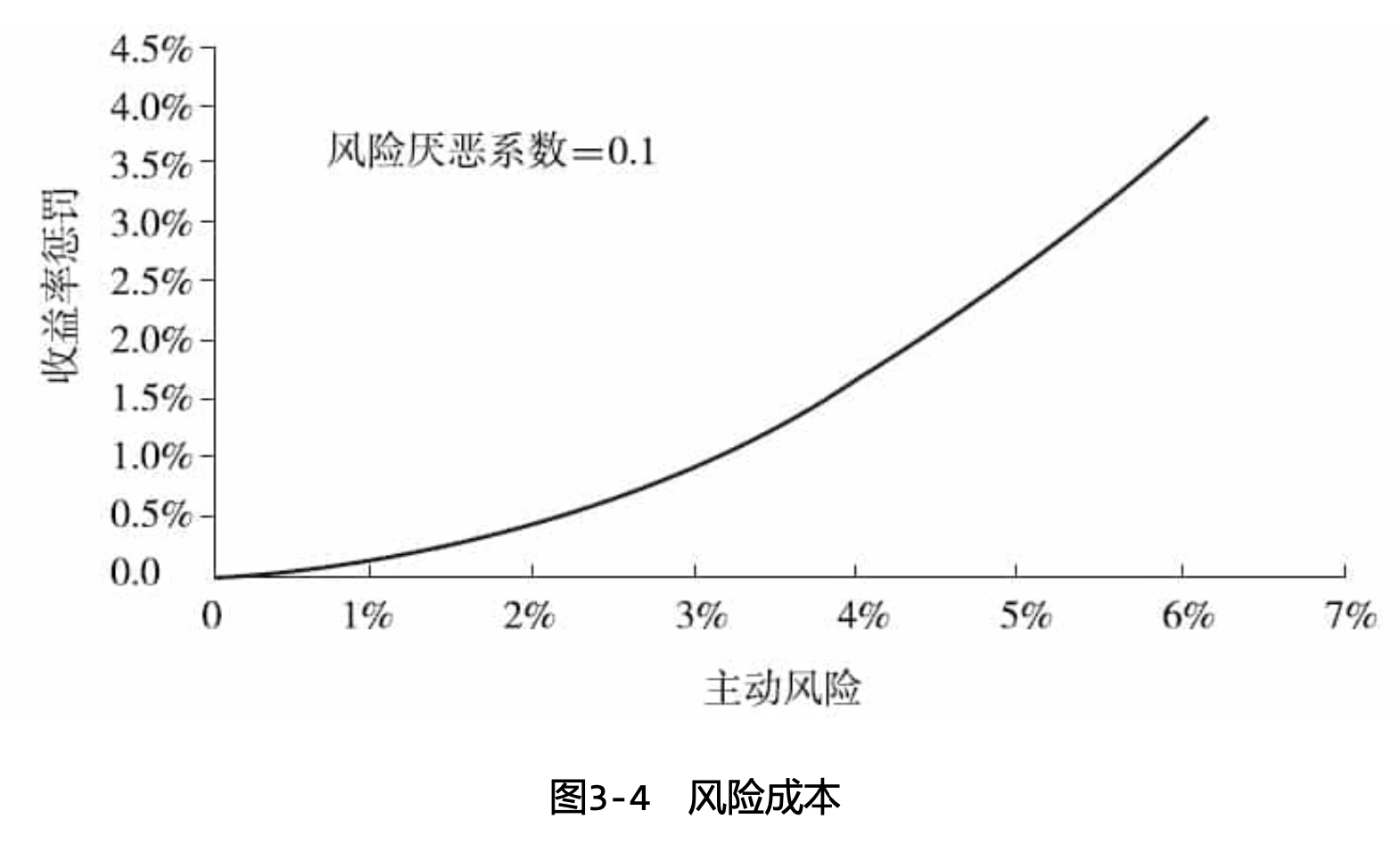
3.7 基本的风险模型

在上一节中我们提到了决定投资组合风险的一个重要问题。对于一个由两只股票构成的投资组合，我们需要这两只股票各自的波动率，以及它们之间的相关系数。更一般地，当组合涉及的股票只数为N时，需要估计的相关系数的个数为N（N-1）/2。

我们可以将所有需要估计的参数总结到一个协方差（covariance）矩阵V中：

其中我们将$r_i$ 和$r_j$ 的协方差表示为$\sigma_{ij}$ ，并且$\sigma_{ij} =\sigma_{ji}$ 。协方差矩阵包含了计算组合层面风险所需的所有资产层面的风险信息。风险模型的目标就是要精确并高效地预测协方差矩阵。协方差矩阵中包含太多的独立参数，这使得建立风险模型的任务极具挑战性。

本节我们考虑三种基本的股票风险模型。

• 第一种是单因子模型，它赋予每只股票两部分风险——市场风险和残差风险。
• 第二种是一个假设任意两只股票之间相关系数相同的模型。
• 第三种是用历史收益率估计协方差矩阵V中每一项的模型。

3.7.1 单因子风险模型

单因子风险模型是CAPM的雏形，但二者仍有不同。单因子风险模型首先将收益率分解为

$r_n = \beta_n \cdot r_M + \theta_n$

其中$\beta_n$是股票$n$的贝塔值，$\theta_n$ 是股票$n$的残差收益率。单因子风险模型假设残差收益率$\theta_n$是互不相关的，因此推出

$Cov\{r_n, r_m\} = \beta_n \cdot \beta_m \cdot \sigma_M^2$

以及

$\sigma_n^2 = \beta_n^2 \cdot \sigma_M^2 + \omega_n^2$

当然，不同股票的残差收益率之间实际上是相关的。事实上，所有股票的残差收益率的市值加权平均值应该精确等于0：

$\Sigma_{n}h_M(n) \cdot\theta_n = 0$

虽然如此，单因子模型依旧很有吸引力，因为它分离了市场风险和残差风险，并将股票之间的残差协方差保守估计为0。

3.7.2 相关性一致模型

第二种基本风险模型需要对每只股票的波动率$\sigma_n$ ，以及股票之间的平均相关系数$\rho$进行估计。这意味着任意两只股票之间的协方差为

$Cov\{r_n, r_m \}=\sigma_n ·\sigma_m ·\rho$

这种模型的最大优点就是简单，因此它适用于“快速但不必精确”的应用。然而，该模型忽略了类似行业或者具有相似属性的股票之间的微妙联系。

3.7.3 历史一致性模型

第三种基本风险模型依赖于历史数据的样本方差和样本协方差；这种估计既不稳健也不合理。在该模型下，我们用T个时期的样本来估计一个N×N的协方差矩阵。如果T≤N，我们将能够构建一个理论上具有零风险的投资组合。因此，历史样本模型要求T>N。如果要估计标普500指数成分股月度收益率的协方差矩阵，这将需要超过40年的数据。并且，即使T超过了N，历史样本模型仍然存在几个问题：

·为了满足T>N的条件，我们只能考虑较短时间尺度上的收益率，例如1天或1周；然而投资经理一般需要更长时间尺度上的预测，例如1个季度或者1年。

·历史风险不能快速反映公司不断变化的基本面，特别是并购拆分（mergers and spinoffs）时会有问题。

·还有选择偏差，例如收购（takeover）、杠杆收购（LBO），或者破产的公司将被忽略。

·样本偏差将导致协方差估计上的某些整体偏差。一个500只资产的协方差矩阵包含125250个独立参数。如果其中5%是不好的估计，那么我们将有6262个不好的估计。

3.8 结构化风险模型

多因子风险模型基于如下想法：股票的收益率可以被一组共同因子和一个仅与该股票有关的特异因子解释。

通过识别出重要的因子，我们可以降低问题的规模。例如，原本要处理6000只股票（18003000个独立的方差和协方差）的情形，利用因子模型可以转化为仅需处理68个因子的问题。即使股票数目发生变化，因子数量也是不变的。当我们只关注少数几个因子并允许股票对这些因子的暴露不断变化时，情况将变得更为简单。

3.8.1 收益率线性分解

结构化风险模型首先对收益率进行简单的线性分解，分解方程中包含四个组成部分：股票的超额收益率、股票的因子暴露、因子收益率以及股票的特异收益率。线性分解的结构如下：

$r_n(t) = \Sigma_kX_{n,k}(t) \cdot b_k(t)+u_n(t)$ (3-16)

式中　$r_n (t)$——资产n从时刻t到时刻t+1的超额收益率（收益率减去无风险收益率）；

$X_{n,k}(t)$——时刻t时，资产n对因子k的暴露度（exposure）。暴露度也经常被称为因子载荷（loading）。行业因子的暴露度要么是0（表示该资产不属于该行业），要么是1（表示该资产属于该行业）。 对于其他共同因子，暴露度通常是标准化的，因此全部股票的平均暴露度为0，并且暴露度的横截面标准差等于1。

$b_k(t)$——因子k从时刻t到时刻t+1的因子收益率；

$u_n(t)$——股票n从时刻t到时刻t+1的特异收益率（specific return），即其总收益率中不能被共同因子解释的部分。我们的风险模型包含了对特异收益率$u_n$ 的风险的预测。

3.8.2 计算协方差矩阵

多因子模型并不蕴含任何意义下的因果关系。模型中的因子可能是，也可能不是证券收益率的驱动力量。在我们看来，它们只代表了我们试图解释风险的维度。

现在我们假设特异收益率与因子收益率不相关，不同股票的特异收益率之间也互不相关。在这个假设和式（3-16）描述的收益率结构下，整个市场的风险结构为：

$V_{n,m} = \Sigma_{k_1,k_2=1}^{K} X_{n,k_1} \cdot F_{k_1,k_2} \cdot X_{m, k_2} + \Delta_{n, m}$

式中　$V_{n,m}$ ——资产n和资产m的协方差。当n=m时，它就是资产n的方差；

$X_{n,k_1}$ ——资产n对因子k 1 的暴露度，定义同上；

$F_{k_1,k_2}$ ——因子$k_1$ 和因子$k_2$ 之间的收益率协方差。当$k_1 = k_2$ 时，它就是因子k的收益率方差；

$\Delta_{n,m}$ ——资产n和资产m之间的特异协方差。我们假设所有资产对之间的特异协方差等于0，所以Δ n，m 在n≠m时总是等于0。当n=m时，它就是资产n的特异方差。

3.8.3 选择因子

寻找因子时只有一个限制条件：所有因子必须都是先验因子（priori factor）。所谓先验因子，是指因子暴露必须在考察期初就能确定

首先，我们可以将因子分为三大类：

• 对外部变化的响应
• 资产属性的横截面比较类因子
• 纯粹的内在或统计因子

响应类因子

响应类因子就试图捕获股票市场和外部经济力量之间应该存在某种可被证实的关联。这些因子包括对以下外部变化的响应：债券市场收益率（相应因子有时被称为债券贝塔）、通胀异动（unexpected changes in inflation/inflation surprise）、油价变动、汇率变动、工业产量变动，等等。这些因子有时也被称为宏观因子。响应类因子的解释力可能非常强，但他们有三个严重缺陷：

第一个缺陷是我们必须通过回归分析或者类似的技术来估计这些响应系数。第二个缺陷是我们的估计通常基于过去5年的历史行为。即使能够在统计意义下精确地捕获过去的情况，这些估计值也可能无法精确描述现在的情况。第三个缺陷是宏观数据通常由政府采集而不能在市场中被直接观测到，因此其质量不佳。这通常意味着不精确的、延迟的以及频率相对过低的观测数据。

横截面比较类因子

横截面比较类因子比较股票的各种属性，与股票之外的经济没有直接联系。横截面属性一般可以归为两类：基本面类和市场类。横截面的意思是某个因子对所有股票的暴露程度之和。

统计因子

关注3条准则的因子：有区分能力（incisive）、直观（intuitive）和有意义（interesting）。有区分能力的因子能区分出收益率特征显著不同的股票群。直观的因子与市场的某个易于理解的或者公认的维度相关；即具有直观的经济含义或可信的故事。有意义的因子能够解释股票表现的某些部分。

常用的因子主要分为两类：行业因子和风险指数

行业因子

行业分类将股票划分为多个互不重叠的类别。行业分类应该满足以下几个原则：

·每个行业都应该包含合理数目的公司； ·每个行业在全市场中都应该占有合理的市值比例； ·行业划分应该符合市场共识及投资者的心理习惯。

行业暴露通常是0/1变量——股票要么属于该行业，要么不属于该行业。市场组合对全部行业因子的暴露度之和等于1。由于大型公司可能在多个行业运作，我们有时将行业因子进行扩展，使它能够处理“单个公司多行业归属”的情况。

风险指数

对一些共同的投资主题的暴露也是股票风险的来源，我们用风险指数因子（risk index factor）来衡量它。

·波动率。按波动率区分股票。在这个维度中排名较高的股票在历史时期上具有较高的波动率，我们也预期它们在未来仍然保持较高的波动率。 ·动能。按近期表现区分股票。 ·规模。按市值大小区分股票。 ·流动性。按交易量的大小区分股票。 ·成长性。按过去和预期的盈利增长区分股票。 ·价值。按基本面情况区分股票，特别有几种常见的比率指标：盈市率（earnings-to-price）、分红率（dividend-to-price）、现市率（cash flows-to-price）、净市率（book-to-price）、销市率（sales-to-price），等等。这些指标反映了股票价格相对于发行公司的基本面而言是便宜还是昂贵。 ·盈利波动率。按盈利的波动性区分股票。 ·财务杠杆。按债务股本比率（debt-to-equity）和对利率风险的暴露度区分股票。

每个股票市场都会根据其自身的独特属性含有多于或少于上述列表中的风险指数。 每一个风险指数都包含若干个具体度量，我们称之为描述变量 （descriptor）。

3.9 风险模型的应用

多因子风险模型可以用于分析当前的组合风险。它不仅能够衡量组合的总体风险水平，更重要的是，它还可以将组合风险分解到各个来源。风险分解识别出投资组合风险的重要来源，使我们能够检查它们是否也是主动收益率的来源。

分解风险的三种方式：

• 将收益率划分为市场部分和残差部分；
• 考察组合相对于某个业绩基准的风险，即分解出主动风险；
• 将组合风险按照多因子模型分解为模型风险和特异风险。

风险分析将主动投资经理承担的风险划分为固有的、意向的和意外的风险。

·固有风险 （inherent）。试图超越某一业绩基准（或市场）的主动投资经理必须承担基准风险，即该业绩基准自身的风险。这部分风险是固有的，是组合投资经理无法控制的。

·意向风险 （intentional）。主动投资经理将超配他看涨的股票，同时低配他看跌的股票，由此产生的风险是组合经理有意承担的，因此称为意向的。在均值/方差有效组合中，预期收益率最高的股票应该对组合风险具有最高的边际贡献（否则可提高预期收益率而不增加风险，与有效性矛盾）。符合自身投资理念的意向风险对主动投资经理而言是一件好事。

·意外风险 （incidental）。这是构建主动头寸时的副产品，投资经理不经意间暴露于某些具有显著主动风险边际贡献的因子。例如，一位通过筛选分红率构建组合的投资经理将在具有较高平均分红率的行业上下很大的意外赌注。这些行业赌注是意向的还是意外的？意外赌注经常因为持续的组合管理产生，一系列股票调整，每一次调整独立地看都是没问题的，但最终却产生了累积的意外风险。

3.10 风险模型的效果

1. 按与实现值的相关性考量，基于投资组合的风险预测远强于基于历史表现的风险预测。
2. 标准差和方差具有很高的持续性。各种备选风险度量并没有展示出方差信息之外的持续性。换言之，研究显示我们不能预测方差之外的风险信息。许多其他研究证实了资产收益率通常具有较宽的分布，说明我们需要预测方差之外的风险信息（例如峰度）。但本项研究考察的是另外一个问题：一个具有较宽分布的投资组合，其较宽分布的特征是否能够持续？这才是投资组合选择中的重要问题，而答案是否定的。

第四章 超常收益率、业绩基准和附加值

4.1 业绩基准

事实上，我们并没有一个包罗万象的市场组合来作为对比基准，即使是通常被用作对比的业绩基准（上证500，标普500等），也只包括市场的一部分。鉴于此，我们将弃用市场 ，转而使用业绩基准这个术语。业绩基准组合还有一些别名，如标杆 和规范组合 。

投资经理的业绩是相对于其基准来衡量的。投资经理的主动收益率是其组合收益率与业绩基准组合收益率之差。

我们可以在CAPM的框架之外定义贝塔。如果$r_B$是业绩基准组合的超额收益率，而$r_n$是股票n的超额收益率，那么我们可以定义$\beta_n$为

$\beta_n = \frac{Cov\{r_n, r_b\}}{Var\{r_B\}}$

我们已经突破了贝塔的标准定义。贝塔不再是一个绝对的量：它不再是相对于市场的贝塔，而是相对于某个业绩基准的贝塔。相应地，残差风险的概念也变为相对的：它不再是相对于市场的残差，而是相对于一个业绩基准的残差。

主动头寸是组合头寸与业绩基准头寸之差。风险资产上的主动头寸$h_{PA}$ 定义为

$h_{PA} =h_P -h_B$ 　（4-2）

同时，主动现金头寸为

主动现金=$h_P(0)-h_B(0)=-e^T \cdot h_{PA}$ 　（4-3）

主动方差 是主动头寸收益率的方差。如果我们用$\psi^2_P$ 表示主动方差，那么

$\psi^2_P =h^T_{PA} ·V·h_{PA} =\sigma^2_P +\sigma^2_B -2·\sigma_{P,B}$ 　（4-4）

如果我们使用相对于业绩基准的贝塔和相对于业绩基准的残差收益率$\theta_P$ ，那么我们可以将主动方差写为

$\psi^2_P =\beta^2_{PA} \cdot \sigma^2_B + \omega^2_P$ 　（4-5）

式中，$\beta_{PA}$ 是主动贝塔（即$\beta_P-1$），$\omega_P$是残差风险：

$Var\{\theta_P\} = \omega^2_P$ 　（4-6）

我们选择的业绩基准将帮助我们把预期收益率分解为不同的组成部分。

4.2 预期收益率的组成

我们可以将预期收益率预测值分解为四部分：无风险部分（时间溢价）、业绩基准部分（风险溢价）、基准择时部分（超常业绩基准收益率）、阿尔法部分（预期残差收益率）。如果$R_n$ 代表资产n的总收益，那么我们可以将$E\{R_n\}$写为

$E\{R_n\}=1+i_F + \beta_n ·\mu_B +\beta_n ·\Delta f_B +\alpha_n$ 　（4-7）

4.2.1 组成部分

时间溢价 $i_F$

这是投资者放弃其他投资一年所获得的回报。它被称为时间溢价，即对时间的补偿。由于我们能够事先获知无风险资产的收益率，因此我们可以事先确定时间溢价。

风险溢价 $\beta_n \cdot \mu_B$

这里我们借用CAPM的概念。分析师通常用极长期（70年以上）平均值（虽然其他估计方法也很常见）来估计业绩基准的预期超额收益率$\mu_B$ 。每年3%~7%的收益率对大多数股票市场而言是一个合理的预期值。注意低贝塔资产具有较低的风险溢价，而高贝塔资产具有较高的风险溢价。

超常业绩基准收益率 $\beta_n ·\Delta f_B$

上述业绩基准预期超额收益率$\mu_B$是基于极长期考虑的，这一项是业绩基准的择时收益。如果你相信下一年（或季度、月）将会有所不同，那么$\Delta f_B$就衡量了业绩基准在临近的未来时期上的预期超额收益率与长期预期超额收益率之差。

残差收益率 $\alpha_n$

阿尔法是预期残差收益率，$\alpha_n =E\{\theta_n \}$。

4.2.2 组合解释

一致预期超额收益 $\beta_n \cdot \mu_B$

对于接受业绩基准是先验有效的投资组合的投资者，他们的预期超额收益率就是一致预期超额收益率。这组预期超额收益率将使投资者选择与业绩基准组合完全匹配的投资组合。

预期超额收益率 $f_n = \beta_n \cdot \mu_B + \beta_n \cdot \Delta f_B + \alpha_n$

预期超额收益率$f_n$，是由风险溢价($\beta_n \cdot \mu_B$)、对超常业绩基准预测的响应($\beta_n \cdot \Delta f_B$)以及阿尔法($\alpha_n$)组成的。

预期超常收益率 $\beta_n ·\Delta f_B +\alpha_n$

预期超常收益率是主动管理的关键。其中第一项$\beta_n ·\Delta f_B$衡量了基准择时收益（注意到预期收益率$\beta_n ·\Delta f_B$将产生一个看多或看空业绩基准的赌注。基准择时这一项更一般地用于讨论多时间段的策略。根据其构造，长期上应该有$E\{\beta_n ·\Delta f_B\}=0$成立，因此$\Delta f_B$将会时正时负。），第二项$\alpha_n$衡量了选股收益。

4.2.3 计算

从一列预期收益率$E\{R_n\}$、资产贝塔值$\beta_n$ 、每只资产在业绩基准中的权重$h_B(n)$、无风险收益率$i_F$ 以及业绩基准的长期预期超额收益率$\mu_B$ 开始，我们可以将预期收益率分解为几个组成部分。

第1步：计算业绩基准的预期超额收益率。

$f_B = \Sigma_n h_B(n) \cdot E\{R_n - (1 + i_F)\}$

第2步：超常业绩基准收益率为

$\Delta f_B = f_B - \mu_B$ (4-9)

4.3 管理总风险和总收益率

现代组合投资理论的传统途径（Markowitz-Sharpe）是在基金经理可获得的机会集中做风险/预期收益率的权衡。

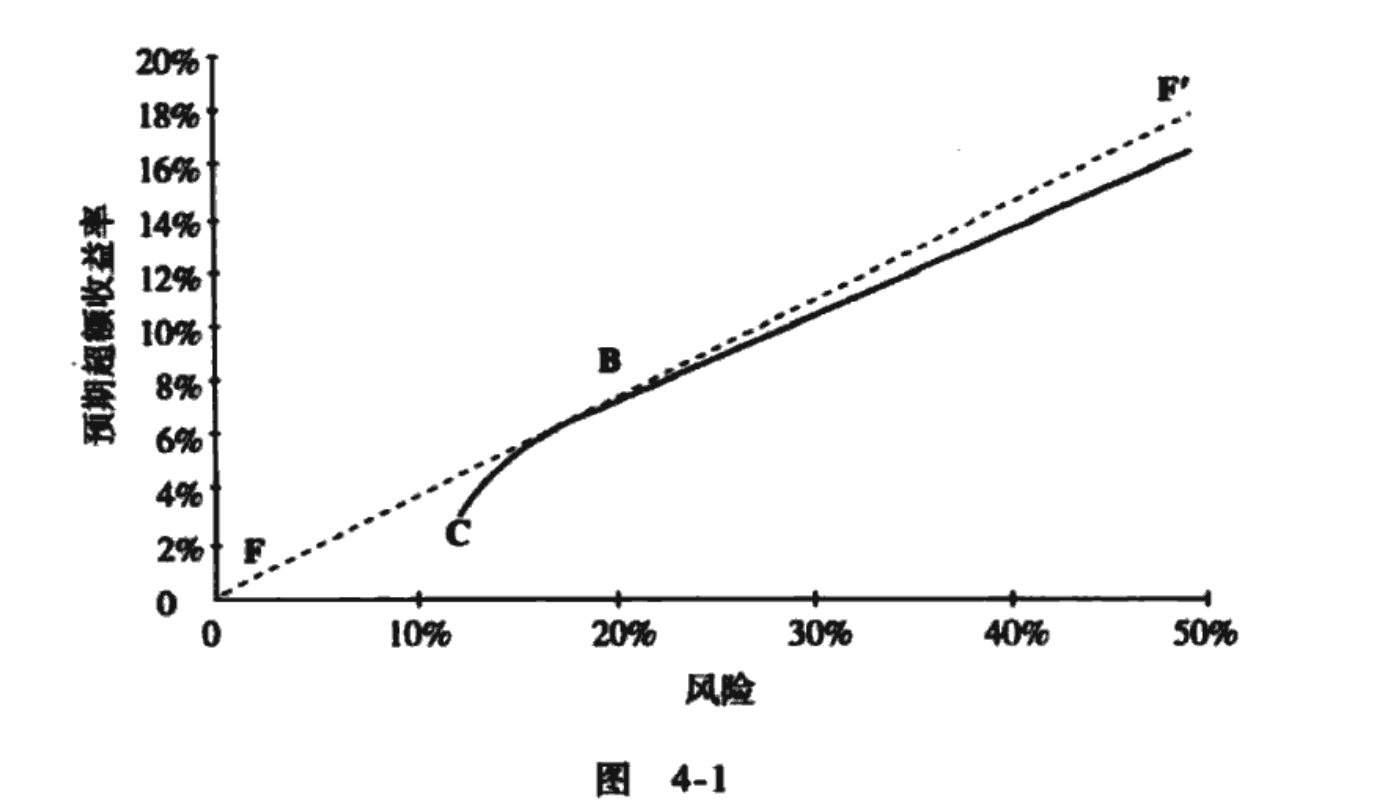
图4-1展示了一致预测下可获得的收益率/风险选择。横轴衡量了组合风险，纵轴衡量了用一致预测$\mu=\beta\cdot \mu_B$ 估计的预期超额收益率。图中双曲线围成的区域描述了全额投资约束下我们可获得的全部“预期超额收益率/风险”组合。具有最高预期超额收益率/风险比率的全额投资组合就是业绩基准B。这并不奇怪，因为一致输入必然会导致一致输出。

主动管理始于投资经理的预测对一致观点的偏离。 如果投资经理对预期超额收益率的预测为f，那么我们将拥有图4-2中所示的风险/收益率选择。在图4-2中，业绩基准不在有效前沿上。一个不同于B的全额投资组合Q具有最高的$f_P /\sigma_P$ 比率。此时，存在战胜组合B的机会！

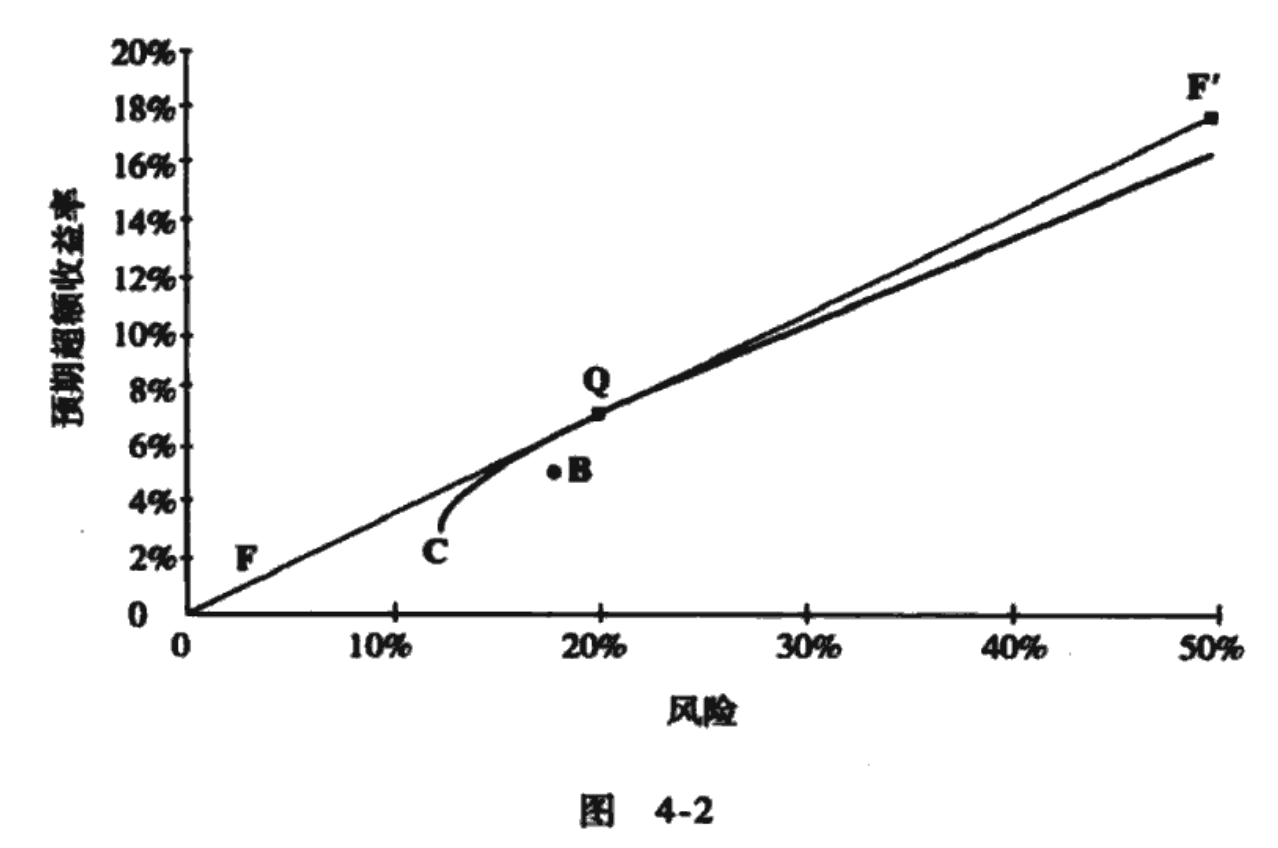
我们可以将股票n的预期超额收益率预测表示为：

$f_n = \beta_n \cdot f_B + \alpha_n$ 　（4-10）

式中，$f_B$ 是业绩基准的预期超额收益率预测，$\beta_n$ 是股票n的贝塔，$\alpha_n$ 是股票n的预测阿尔法。$f_n$ 偏离一致预测的程度由$f_B$ 偏离一致预测$\mu_B$ 的程度和$\alpha_n$ 偏离零的程度决定。

4.3.1 总收益率/总风险 权衡

挑选出怎样的投资组合依赖于我们的目标。传统途径使用均值/方差目标函数来指导组合挑选。我们将这一衡量标准称为预期效用，表示为$U[P]$，定义为

$U[P] = f_P - \lambda_T \cdot \sigma_P^2$ (4-11)

式中，$f_P$ 是预期超额收益率，$\lambda_T \cdot \sigma^2_P$ 是一个风险惩罚项。参数$\lambda_T$ 衡量了对总风险的厌恶程度，这里的总风险包括系统性风险（源自业绩基准）和残差风险（源自资产选择）。有些人习惯于采用风险接受系数$\tau$来代替风险厌恶系数$\lambda$，这二者是等价的，$\tau = \frac{1}{\lambda}$。

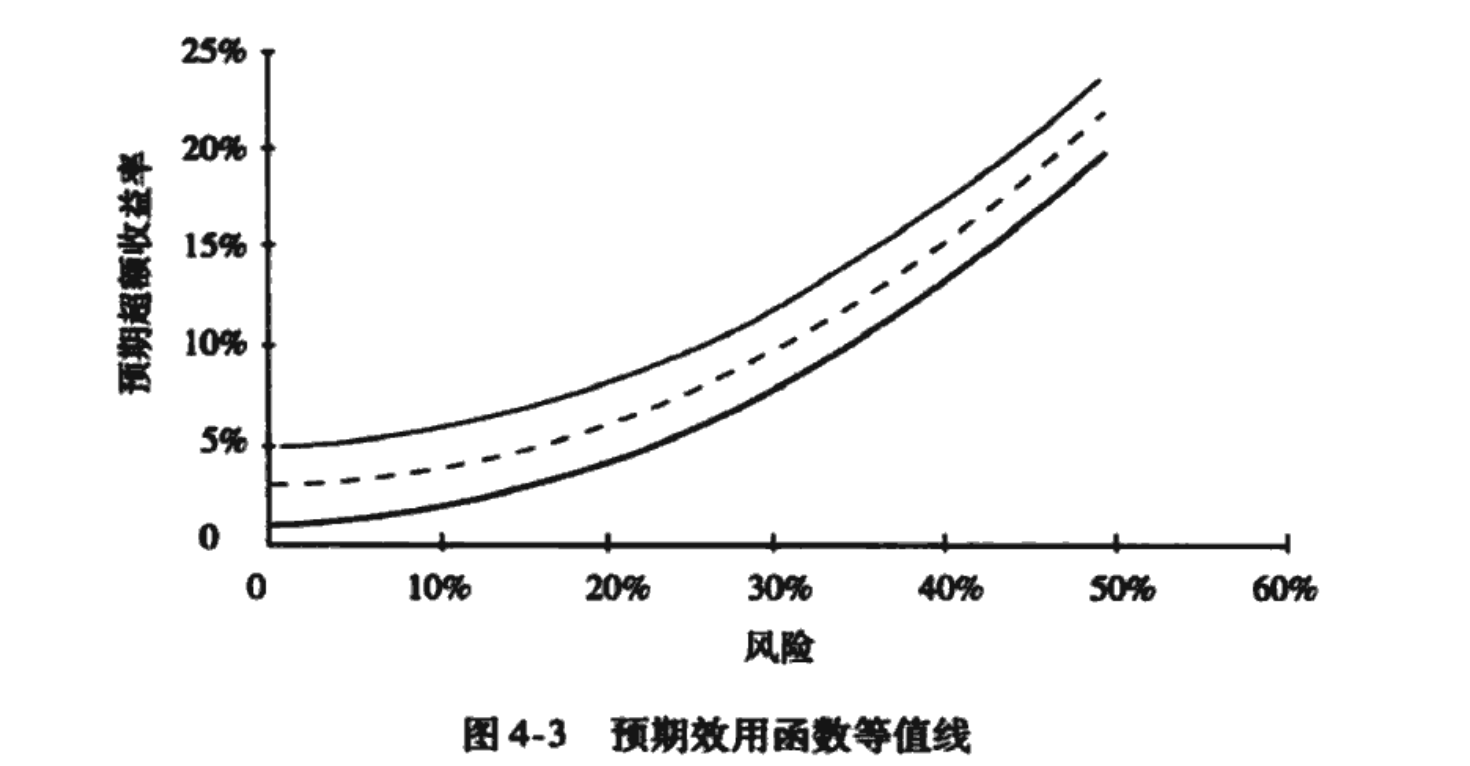
图4-3的看法是，$f_P = U[P] + \lambda_T \cdot \sigma_P^2$，因此是一个开口向上的抛物线。

还有一种更科学的确定$\lambda_T$合理数值的方式。考虑一种我们没有额外信息的情形，即$f=\mu$，我们的预测等于一致预测。预期业绩基准超额收益率是$μ_B$ ，业绩基准风险是$\sigma_B$ 。考虑如何混合业绩基准组合B和无风险资产F的简单问题。预期超额收益率将是$\beta_P \cdot \mu_B$ ，其中$\beta_P$ 是对基准组合的投资比例。风险将是$\beta^2_P \cdot \sigma^2_B$ 。目标函数为$\beta_P \cdot \mu_B - \lambda_T \cdot \beta^2_P \cdot \sigma^2_B$ ，取极值的时候我们有其导数 $\mu_B-2·\lambda_T·\beta_P·\sigma^2_B=0$，当式（4-12）成立时，最优解将为$\beta_P=1$。

那么导致我们选择业绩基准组合的总风险厌恶系数为 $\lambda_T = \frac{\mu_B}{2\sigma_B^2}$

最优组合P的贝塔为：$\beta_P = \frac{f_B}{2 \lambda_T \sigma_B^2} = 1 + \frac{\Delta f_B}{\mu_B}$

在总风险/总收益率分析框架下，较低水平的信息也会导致很高水平的残差风险。因此我们需要一种基于收益率的指标，来权衡主动风险和主动收益率，这就是附加值。

4.4 附加值

主动投资经理的目标函数将风险和收益率拆分为三个部分：

内蕴部分 ，$f_B -\lambda_T · \sigma^2_B$ 。内蕴部分源自业绩基准的风险和收益率，它不在投资经理的掌控范围内。注意我们用$\lambda_T$表示我们对总风险的厌恶系数。

择时部分 ，$\beta_{PA} ·\Delta f_B - \lambda_{BT} ·\beta^2_{PA} ·\sigma^2_B$ 。这是业绩基准择时产生的贡献，它由投资经理的主动贝塔决定。注意我们用$\lambda_{BT}$ 表示我们对业绩基准择时风险的厌恶系数。

残差部分 ，$\alpha_P -\lambda_R ·\omega^2_P$ 。这是由投资经理的残差头寸产生的。注意我们用$\lambda_R$ 表示我们对残差风险的厌恶系数。

目标函数的后两部分衡量了投资经理增加价值的能力，我们称之为附加值 （value added，VA）

$VA=\{\beta_{PA} ·\Delta f_B -\lambda_{BT} ·\beta^2_{PA} ·\sigma^2_B \}+\{\alpha_P -\lambda_R ·\omega^2_P \}$　（4-15）

附加值目标函数中的两个组成部分与式（4-11）中的均值/方差效用目标函数类似。每个组成部分都由一个预期收益率项和一个方差项构成。业绩基准择时风险厌恶系数$\lambda_{BT}$ 和残差风险厌恶系数$\lambda_R$ 将方差转化为从预期收益率中扣减的惩罚项。附加值是一种风险调整预期收益率，它忽略了业绩基准对风险和预期收益率的贡献。

业绩基准择时

业绩基准择时是指逐个时期选择合适的主动贝塔，选择最佳的业绩基准择时，可以最大化附加值的第一项，此时的主动贝塔为：

$\beta_{PA} = \frac{\Delta f_B}{2 \cdot \lambda_{BT} \cdot \sigma^2_B}$

4.5 主动收益率与残差收益率

怎样将后者与投资经理追求显著主动收益率的目标联系起来呢？

残差收益率和风险为

$\theta_P =r_P -\beta_P · r_B$ 　（4-17） $\omega_P =Std\{\theta_P \}$　（4-18）

而主动收益率和风险为

$r_{PA} = r_P - r_B = \theta_P + \beta_{PA} \cdot r_B$ (4-19) $\psi_P = Std\{r_{PA}\} = \sqrt{\omega^2_P + \beta^2_{PA} \cdot \sigma^2_B}$ (4-20)

只要投资经理避免业绩基准择时，并设置$\beta_P =1$，那么主动收益率（风险）和残差收益率（风险）就是相同的。这是大多数机构股票投资经理采取的做法，并且这样做是有充分理由的，相关原因将在第6章中讨论。如果投资经理确实进行了业绩基准择时，那么从式（4-19）中可以看出，主动收益率等于残差收益率与业绩基准择时收益率之和。

第五章 残差风险和残差收益率：信息率

本章要点： ·信息率 衡量后验的业绩（向过去看）并意味着先验的机会（向未来看）。 ·信息率定义了残差前沿 ，即主动投资经理的机会集（可行域）。 ·每位投资经理的信息率及残差风险厌恶水平决定了他的激进程度（残差风险水平）。 ·我们可以基于直觉 确定信息率和残差风险厌恶系数的合理数值。 ·附加值 依赖于投资经理的机会集和激进程度。

本章首先定义全书的核心概念“信息率”。在本章中，我们主要使用信息率的先验形式（希望是永恒的）。先验信息率指示出主动投资经理的机会集——残差前沿。在第4章中，我们为主动投资经理定义了权衡风险和收益的目标函数。投资附加值源自我们的机会集（信息率）与我们的目标函数之间的交互关系。

5.1 定义阿尔法

向未来看（先验），阿尔法是对残差收益率的预测。向过去看（后验），阿尔法是实现的残差收益率的平均值。

术语阿尔法 和术语贝塔 一样，源自使用线性回归将组合收益率分解为与业绩基准完全相关的部分和与业绩基准不相关的残差部分。如果$r_P(t)$是投资组合在时期$t=1，2，…，T$上的超额收益率，$r_B(t)$是业绩基准在同样时期上的超额收益率，那么回归模型为：

$r_P(t)=\alpha_P +\beta_P · r_B(t) +\epsilon_P(t)$　（5-1）

利用回归分析得到的$\beta_P$ 和$\alpha_P$ 的估计值称为实现的或历史的贝塔和阿尔法。组合P的残差收益率是

$\theta_P(t)=\alpha_P +\epsilon_P(t)$　（5-2）

式中，$\alpha_P$是平均残差收益率，$\epsilon_p(t)$是残差收益率中均值为零 的随机项。

因此，当我们向未来看时，阿尔法是对残差收益率的预测，我们有

$\alpha_n =E\{\theta_n\}$　（5-3）

阿尔法具有投资组合属性，因为残差收益率和数学期望都具有投资组合属性。 考虑一个包含两只股票的简单情形，设两只股票的阿尔法分别是$\alpha_1$ 和$\alpha_2$。如果我们持有一个仅由这两只股票构成的组合，其中股票1的持仓权重为$h_P(1)$，股票2的持仓权重为$h_P(2)$，那么该组合的阿尔法将是

$\alpha_P =h_P(1)· \alpha_1 +h_P(2)·\alpha_2$　 （5-4）

即该组合的预期残差收益率的预测值是$\alpha_P$ 。

根据定义，业绩基准组合的残差收益率总等于零，即$\theta_B =0$总是成立。因此，业绩基准组合的阿尔法必然等于零，即$\alpha_B =0$。为了保证$\alpha_B =0$，我们要求股票层面的阿尔法列向量满足业绩基准中性的约束。

5.2 信息率

5.2.1 后验信息率：对业绩的衡量

信息率（information ratio），用IR表示，是（年化）残差收益率对（年化）残差风险的比值。在后验情形中，我们考虑的是某段历史时期上实现的残差收益率的信息率，即实现的残差收益率除以为获得该收益率所承担的残差风险。

实现的信息率可能（经常）是负值。别忘记业绩基准的信息率必然精确等于零。

5.2.2 先验信息率：对机会的衡量

现在我们向未来看。信息率是每承担一个单位年化残差风险所能获得的预期年化残差收益率。 不过，这里隐含假设了信息被有效利用。因此，信息率更精确的定义是投资经理能够获得最高的年化残差收益率/残差风险的比率。

信息率具有均值为零的对称分布。这与我们对主动管理的基本理解——主动管理是一个零和游戏——是相符的。

现在我们以更正式的形式定义信息率。给定每只股票的阿尔法，任意（随机）投资组合P将具有一个组合阿尔法$\alpha_P$ 和一个组合残差风险$\omega_P$ 。我们定义投资组合P的信息率为

$IR_P = \frac{\alpha_P}{\omega_P}$

• 可以看出，我们的信息率是根据我们的阿尔法优化出来的最优组合来衡量的。
• 无论风险水平怎样变化，收益率与风险的比率总是保持恒定并等于信息率。
• 信息率不依赖于投资经理的激进程度。
• 虽然信息率不依赖于激进程度，但它依赖于时间尺度：预期收益率和方差都随时间尺度的长度增长。因此风险（即标准差）将随着时间的平方根增长，从而预期收益率（随时间增长）与风险（随时间的平方根增长）的比率将随时间的平方根增长。

5.3 残差前沿：投资经理的机会集

主动投资经理的机会集更容易从阿尔法和残差风险的权衡取舍中看出。残差前沿描述了主动投资经理的机会集。先验信息率决定了主动投资经理的残差前沿。

$\alpha_P = IR \cdot \omega_P$ （5-7）

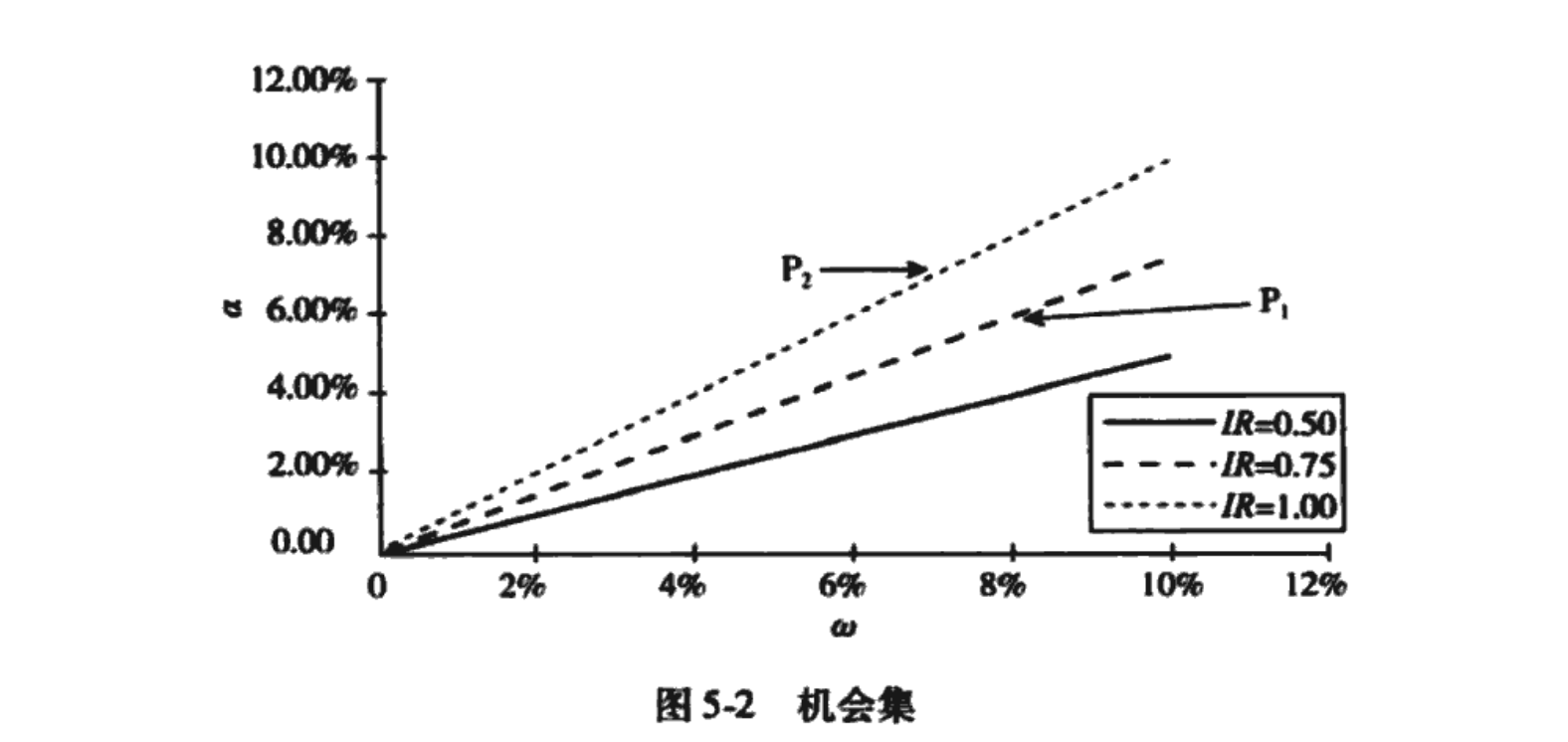
在最优情形下（即沿着残差前沿），投资经理只能通过增加相应程度的残差风险来增加预期残差收益率。

5.4 主动投资经理的目标函数

5.4.1 附加值函数

主动管理的目标（根据第4章）是最大化残差收益率附加值，其中附加值定义为

$VA[P]=\alpha_P -\lambda_R · \omega^2_P$ 　（5-8）

上述目标函数中，预期残差收益率是得分项，残差风险是扣分项。参数$\lambda_R$ 衡量了对残差风险的厌恶程度；它将残差风险折合为阿尔法上的损失。附加值的等值面是联系预期残差收益率$\alpha_P$ 与残差风险$\omega_P$ 的方程，是一族抛物线。在图5-4中我们绘制了三条这样的抛物线，分别对应2.5%、1.4%和0.625%的附加值。

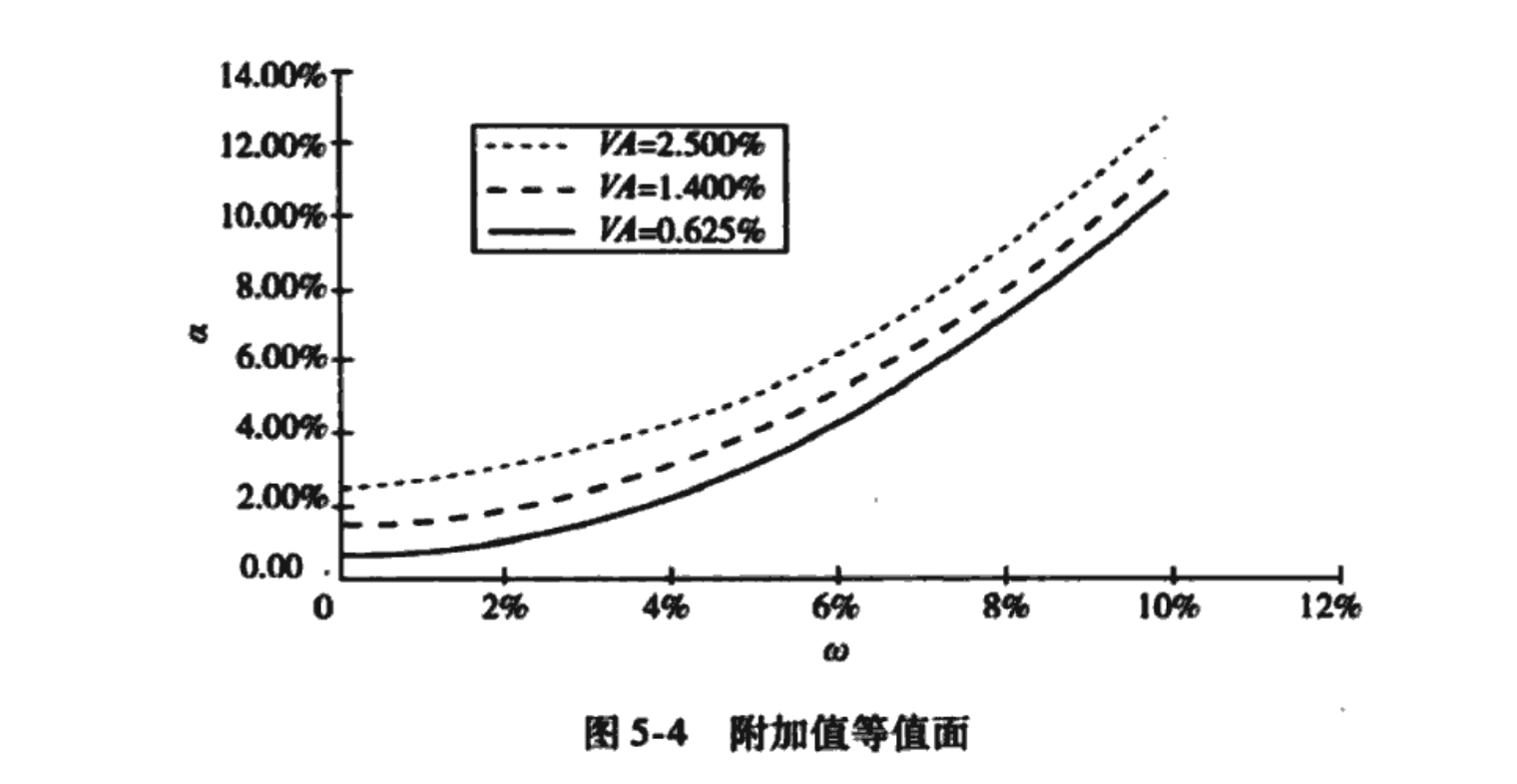
同理，图5-4的看法是 $\alpha_P = VA[P] + \lambda_R \cdot \omega^2_P$，因此是一个开口向上的抛物线。

我们有时也把附加值称为确定性等价收益率 。给定风险厌恶系数$\lambda_R$ ，投资者将把收益率为$\alpha_P$ 、风险为$\omega_P$ 的投资与具有确定性收益率$\alpha_P -\lambda_R ·\omega^2_P$ 的无风险投资视为效用等同。

5.4.2 偏好与机会集的相交

信息率描述了主动投资经理可选的机会集。主动投资经理应该探寻其机会集中的各种选择，挑选附加值最大的那个投资组合。

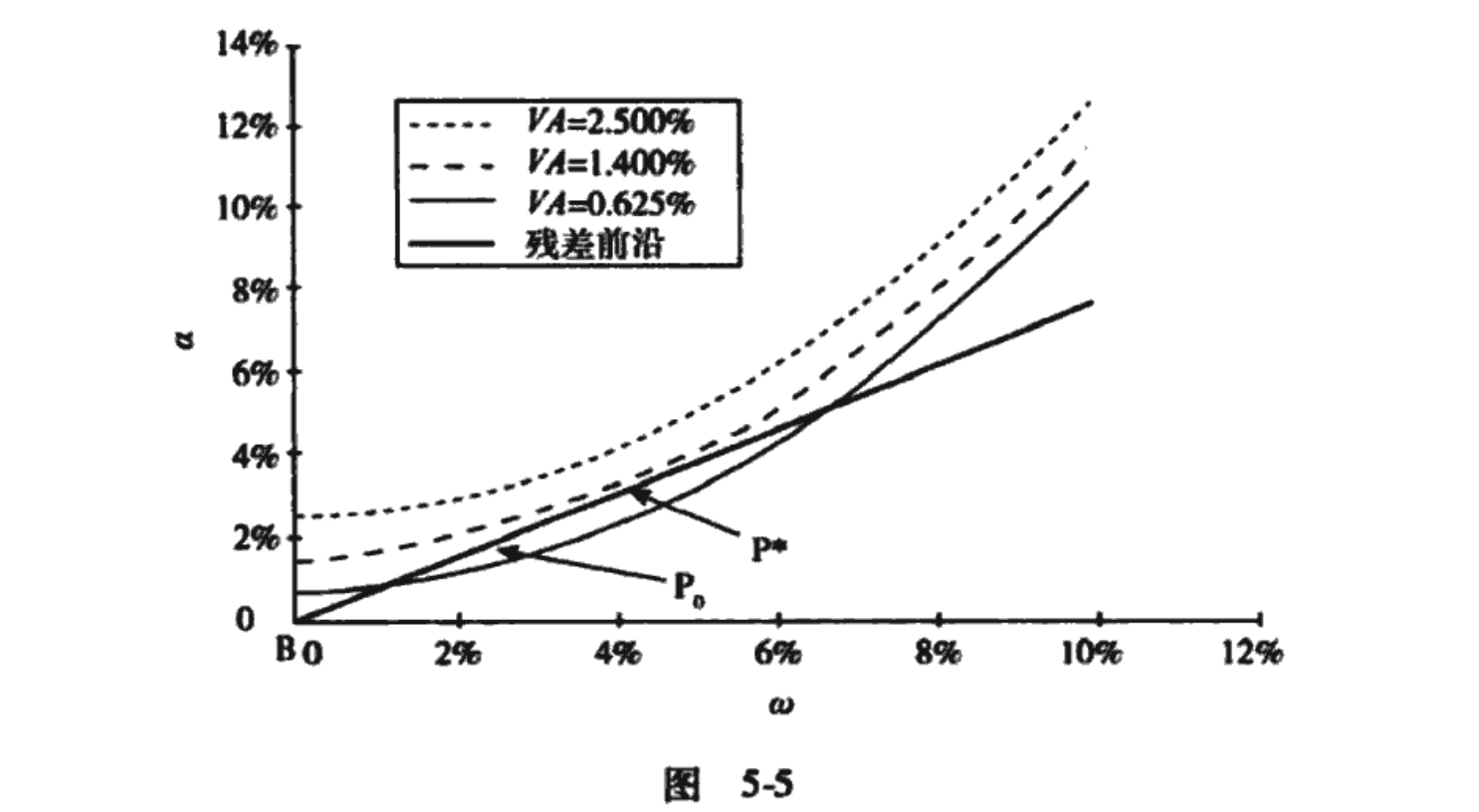
图5-5展示了这一情形。残差前沿对应于信息率等于0.75的情形，而残差风险厌恶系数取λ R =0.1。我们的偏好由三条偏好曲线描述，依次对应于0.625%、1.4%和2.5%的风险调整收益率。附加值VA=1.4%的曲线刚刚好，它与我们的残差前沿恰好相切，切点处是组合$P^*$ 。根据我们的机会集，我们无法比$P^*$ 做得更好，因为任何附加值高于1.4%的曲线都落在我们的机会集之外。因此，组合$P^*$ 是我们的最优选择。

5.4.3 激进程度、机会集和残差风险厌恶

投资经理的信息率和残差风险厌恶水平通过一种简单的关系决定了该经理的最优残差风险水平或激进程度。

投资经理通常会选择残差前沿上的某个投资组合（这一问题的正式表述是“在约束$\alpha/\omega \leq IR$下，最大化$\alpha - \lambda·\omega^2$ ”。由于我们清楚其中的不等式约束在最优解处应该是紧的（即等号成立），所以我们可以将它替换为等式约束，并用来消去目标函数中的α。）。那么唯一的问题就是投资经理的激进程度应该是多少。在投资经理的目标函数（式（5-8））中使用“预算约束”（式（5-7）），我们得到

$VA[\omega_P]=\omega_P ·IR-\lambda_R ·\omega^2_P$ 　（5-9）

这样我们就把这个问题转化为仅涉及残差风险$\omega_P$ 的一个无约束优化问题。当我们提高风险时，预期收益率和风险惩罚会同时增加。而如图5-6所示，这是一个开口向下的抛物线，因此我们可以很快找到极值点和极值。

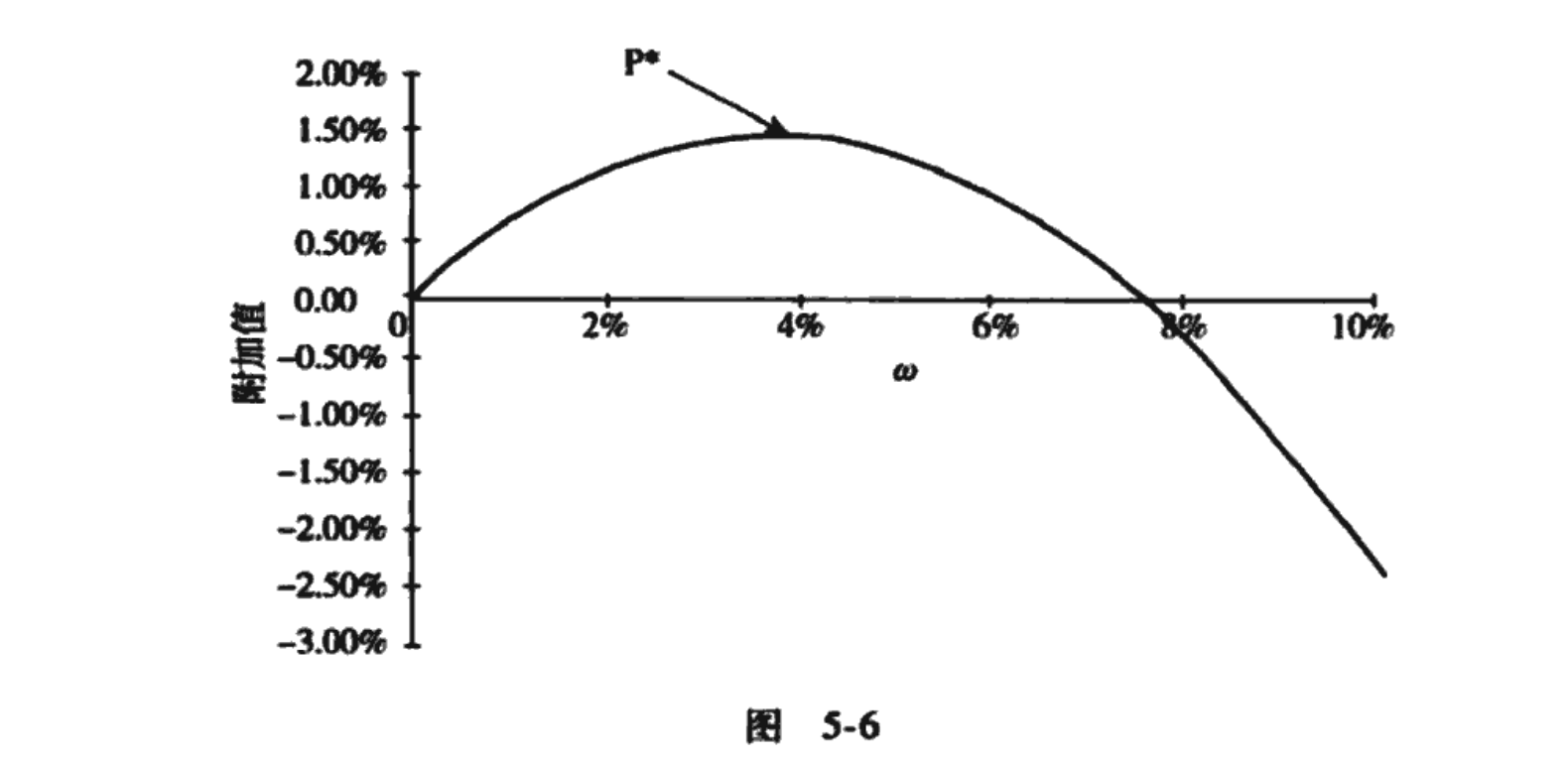
使附加值VA最大化的最优残差风险水平$\omega^*$ 是

$\omega^* = \frac{IR}{2 \cdot \lambda_R}$

此时附加值的极大值为：

$VA^* = VA[\omega^*] = \frac{IR^2}{4\lambda_R} = \frac{\omega^*\cdot IR}{2}$

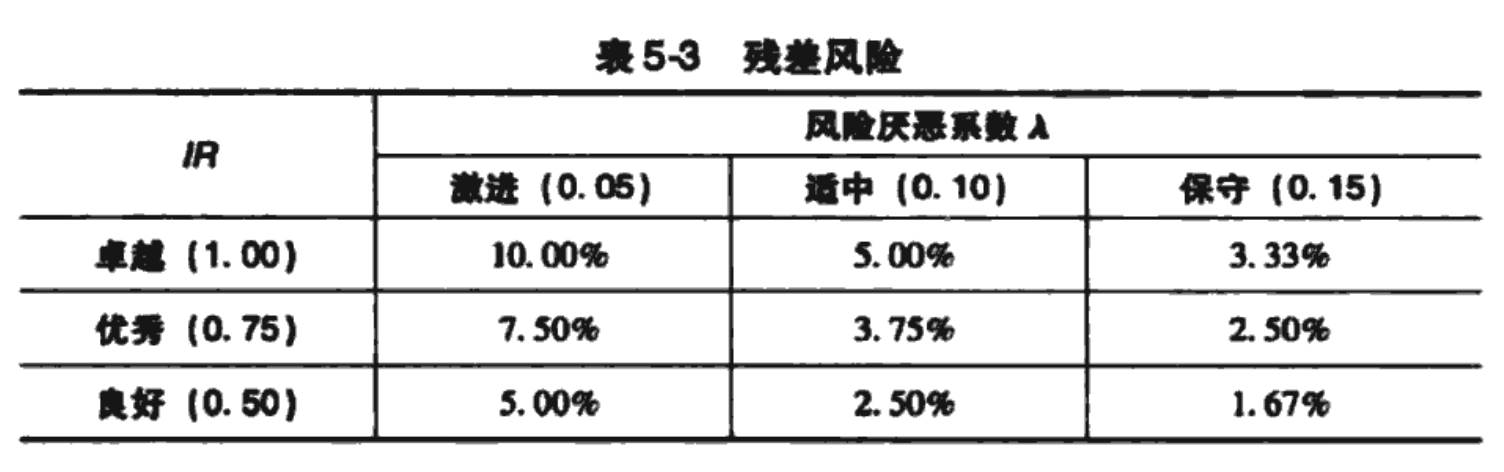
表5-3展示了在几种典型的信息率和残差风险厌恶系数下，最优残差风险水平的变化。信息率选择了三种可能水平：0.50（良好）、0.75（优秀）、1.0（卓越）。残差风险厌恶系数也选择了三种可能水平：0.05（激进）、0.1（中等）、0.15（保守）。

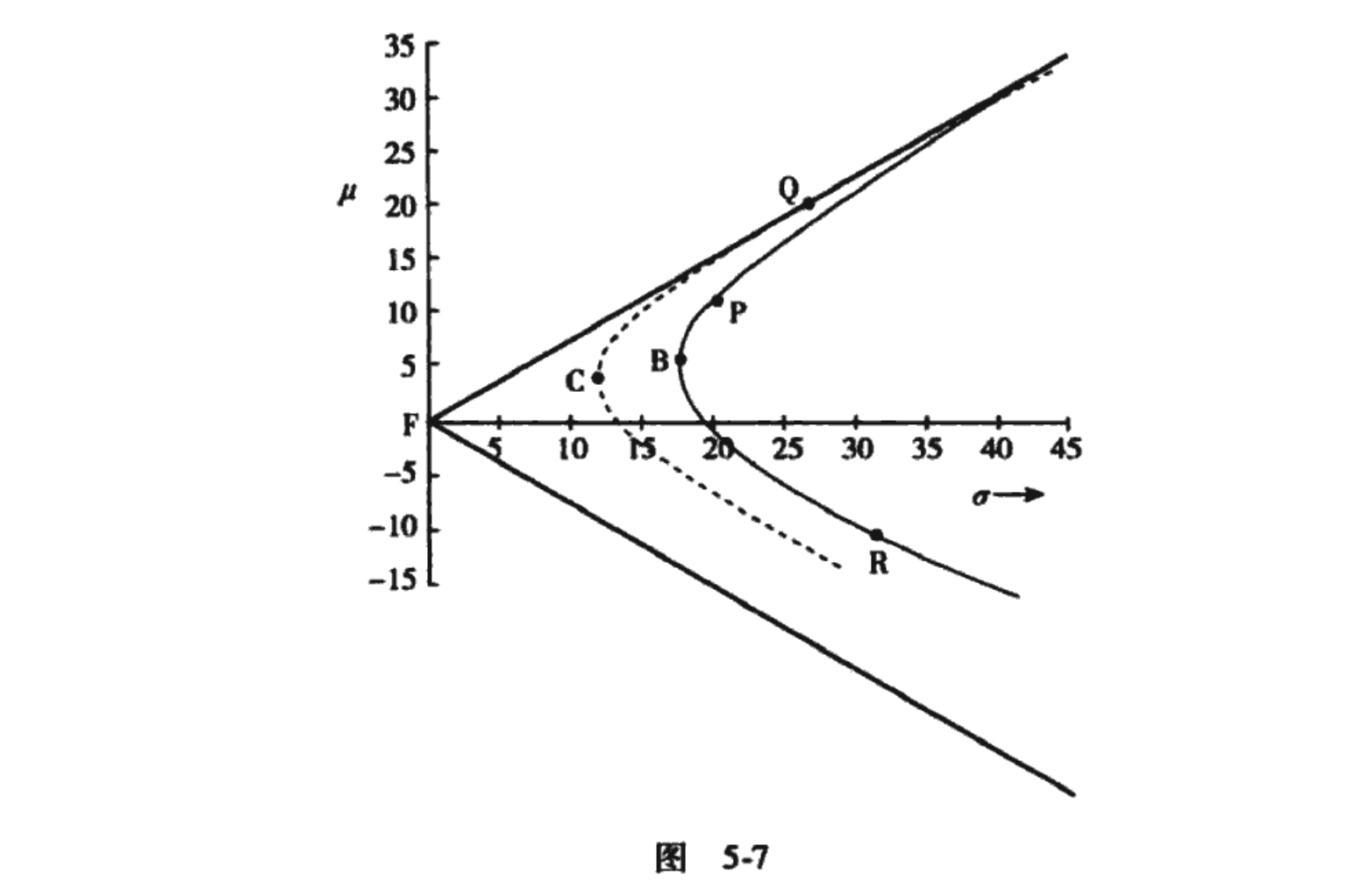
5.5 贝塔=1前沿

残差风险/残差收益率机会集在总风险/总收益率图中会是什么样子的？我们挑选的投资组合（假设不做任何择时）将落在β=1前沿 上。β=1前沿是由全体具有单位贝塔值的有效组合构成的曲线，其中“有效”是指它们在各自预期收益率水平上是具有最小风险的单位贝塔值组合。

Beta=1前沿，也称为马科维茨前沿（Markowitz Frontier），是指资产组合理论中的一种概念，表示在给定的一组风险和收益率下，所有风险和收益率的组合中，风险与收益的平衡点。

具体而言，假设我们有n种不同的资产，每种资产的收益率和风险度量（例如标准差）都已知。根据资产组合理论，我们可以找到所有可能的资产组合，并计算每个组合的预期收益率和风险度量。

当我们将所有可能的资产组合绘制成收益率-风险度量的二维坐标系时，所有组合构成了一个曲线，这个曲线就是Beta=1前沿。这条曲线上的每个点表示一个资产组合，其风险和预期收益率的平衡点是相同的。在这条曲线上，我们可以找到最优的资产组合，即在给定的风险度量下获得最高的预期收益率，或在给定的预期收益率下承受最低的风险。

5.6 直接预测阿尔法

通过少量工作产生一组初步的阿尔法值并不非常困难。一种产生初步阿尔法的方法就是从一组预期收益率开始，然后顺次执行第4章中描述的复杂流程。另一种方法是跳过中间步骤，直接预测阿尔法。

下面我们给出一个能够体现上述想法的例子，它将一组简单的股票排名转化为阿尔法预测。首先，将资产按排名划分为五档：强烈推荐买入，买入，持有，卖出，强烈推荐卖出。给这五档股票依次分配2%，1%，0%，-1%和-2%的阿尔法值。然后计算业绩基准组合的平均阿尔法。如果它等于零，流程结束；如果它不等于零（并没有机制保证它等于零），则对这组阿尔法值进行修正——在每只股票的原阿尔法值中减去业绩基准阿尔法值与该股票贝塔值的乘积。

这些修正后的阿尔法值将是业绩基准中性的。在无约束情形下，它们将引导投资经理持有一个贝塔值等于1.00的投资组合。我们还可以考虑上述示例流程更加精细的版本。例如，我们可以首先将股票划分到若干个经济板块中，然后在每个板块内按排名划分为强烈推荐买入、买入、持有、卖出、强烈推荐卖出这五档。

上述示例说明了两件事。第一，我们不需要激光般精确的阿尔法预测。 我们将在第6章“主动管理基本定律”中看到，即使是最成功的阿尔法预测者，其精确度一般也是相对较低的。只要方向正确，任何保持流程简单性的做法都很可能弥补在阿尔法预测精度上的损失（精度损失通常在小数点后第2位或第3位上）。第二，正确地预测阿尔法可能很难，但直接预测阿尔法并不难。

第六章 主动管理基本定律

本章主要观点：

·投资策略的广度（breadth）就是它每年作出的独立的主动投资决策的数目。 ·投资经理的能力（skill）用信息系数来衡量，就是预测值和实现值之间的相关系数。 ·主动管理基本定律利用广度和能力来解释信息率。 ·主动管理基本定律的可加性，能够把投资策略的附加值归因到其各个组成部分上。

主动投资经理的信息率由它的两个组件决定：投资经理的能力（IC）与策略的广度（BR）。这两个组件进而通过一个简单公式（式（6-3））决定了投资策略的附加值。

这个结果依赖于三条假设。第一条也是最重要的一条是，我们假设投资经理能够精确衡量自己的能力，并能够以最优的方式利用信息。第二，我们假设信息的来源是相互独立的，即投资经理不会对同一信息的不同包装重复下注。第三，我们假设每一个预测的能力IC是相同的。第一条假设可以被称为“胜任”或“完美胜任”假设，它是最为重要的。投资经理需要对自己知道什么以及不知道什么——尤其是后者——有准确的认识。此外，他们还需要知道怎样将他们的想法转化为具体的投资组合，进而从他们的洞察力中获利。后两条假设只是用来简化问题的，并且可通过前面提到的一些方法来减弱其影响。

本章传递的信息很清楚：为了赢得主动投资管理这场游戏，你必须玩得频繁、玩得出色。胜出的诀窍是，你只需要中等程度的预测能力，同时尽可能提高策略的广度——尽可能频繁地将能力应用到足够多的股票上。

6.1 基本定律

信息率衡量了主动投资经理的机会集。假设投资经理能够以均值/方差有效的方式利用其机会集，那么该经理的附加值将正比于其信息率的平方。

基本定律通过以下（近似成立的）公式将广度、能力与信息率联系在一起：

$IR = IC \cdot \sqrt{BR}$ (6-1)

·BR（breadth）：投资策略的广度。广度定义为策略每年对超常收益率作出的独立预测的数目。

·IC（information coefficient）：投资经理的信息系数 。信息系数定义为每个预测与实现结果之间的相关系数。为了简化分析，我们假设所有预测的IC是相同的。

这条定律基于投资策略的两个属性：广度和能力。投资策略的广度是它每年作出的独立投资决策的数目；投资策略的能力以信息系数来衡量，代表了这些投资决策的质量。

在第5章中，我们建立了残差风险水平与信息率之间的关系（式（5-10））。借助于主动管理基本定律，我们可以用能力和广度来重新表达上述关系：

$\omega^* = \frac{IR}{2\lambda_R} = \frac{IC \cdot \sqrt{BR}}{2 \lambda_R}$

我们看到，最优的激进程度正比于能力，同时也正比于广度的平方根。广度越高，我们就有越多的机会在不同的主动赌注之间分散风险，从而可以适当增加整体激进水平$\omega^*$ 。能力越高，我们成功的概率就越大，预期收获也越大，因此我们愿意承担更多风险。

投资经理能创造的附加值依赖于他的信息率（式（5-12））。我们可以将投资经理创造附加值的能力表述为能力和广度的函数：

$VA^* = \frac{IR^2}{4 \lambda_R} = \frac{IC^2\cdot BR}{4 \lambda_R}$

投资策略创造的附加值（风险调整收益率）随着它的广度和能力的平方增长。

6.2 可加性

基本定律在信息率平方上具有可加性，也就是在附加值的维度是可加的，这和我们的直觉是相符的。

假设有两类股票，第一类包含$BR_1$ 只股票，并且我们对第一类股票的预测能力为$IC_1$ ；第二类包含$BR_2$ 只股票，并且我们对第二类股票的预测能力为$IC_2$ 。那么将第一类和第二类股票汇总，将产生如下信息率：

$IR^2 =BR_1 ·IC^2_1 +BR_2 ·IC^2_2$ 　（6-7）

基本定律还有其他的应用。最值得注意的是用它来调整阿尔法的量级，即使得股票超常收益率的预测值与投资经理的信息率相匹配。这一点将在第14章“组合构建”中讨论。

6.3 假设

正如其他理论一样，主动管理基本定律也基于一些不太实际的假设，稍后我们将讨论这些假设。然而，定律蕴含的基本真知是清晰的：要想获得最高的附加值，就要做得频繁（高广度BR）并且做得出色（高能力IC）。

第一个假设是：各个预测之间应该是独立的。

这意味着预测2的信息源不应与预测1的信息源有相关性。例如，假设我们的第一个预测基于假设“成长股将表现较差”，第二个预测基于假设“高分红率股票将表现较好”。这两条信息之间不是独立的；因为成长股倾向于具有极低的分红率，而高分红率股票很少是成长股。这说明我们只是采用了两种方法来描述同一种现象。独立预测的例子是：每个季度调整一次组合的贝塔值，使之从1.00被调整到0.95或者1.05，并且每个季度的择时决策是基于该季度的新信息的。

我们可以通过一个例子来感受信息源之间的相关性会如何降低你的整体能力。假设有两个信息源。独立使用时，每个信息源都具有能力IC，即它们各自的收益率预测值与实现值的相关系数都等于IC。当这两个信息源具有相关性时，来自第二个信息源的信息将不再是全新的。第二个信息源的信息中，有一部分只是加强了我们从第一个信息源获得的信息，另一部分则是新的或增量信息。我们想要找出增量信息的价值。可以想象，两个信息源的相关性越高，增量信息的价值越低。如果用$\gamma$来表示两个信息源之间的相关系数，那么合并信息源的能力$IC_{合并}$ 将是

$IC_{合并} = IC \cdot \sqrt{\frac{2}{1+ \gamma}}$

基本定律基于的另一个假设是：BR个主动赌注中的每一个都具有相同的能力。

事实上，投资经理在不同领域的能力往往是不同的。我们可以从可加性原则（式（6-7））中看出，总体信息率平方等于每个具体领域信息率的平方和。

基本定律的最强假设是：投资经理能够精确估算信息的价值并以最优的方式利用这些信息构建投资组合。 做到这一点需要洞察力和谦逊，但很少有人能够同时具备这两种素质。

6.4 不是大数定律

大数定律告诉我们大样本的均值将十分接近于真实均值，并且随着样本量的增加，样本均值对真实均值的逼近将越来越精确。

基本定律告诉我们：在保持能力不降的前提下，广度越高越好。然而，定律在广度为10和广度为1000时具有等同的有效性；信息率都是$IR = IC \cdot \sqrt{BR}$